Shiguang Deng

Shiguang Deng

Assistant professor at University of Kansas

Posts by Collection

portfolio

Research Thrust One: Design Acquisition

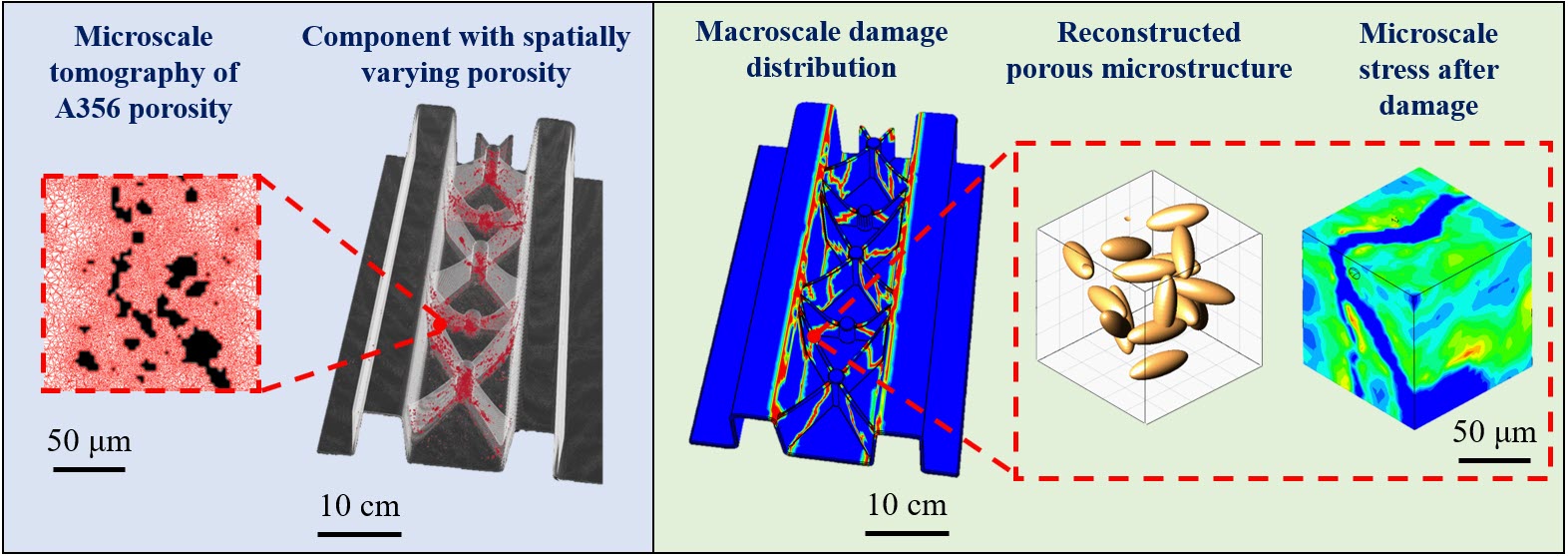
Microstructure Reconstruction: As process-induced material defects are stochastic and inevitable, how can we efficiently represent them in microstructures? To answer this, we applied microstructure reconstruction to characterize tomography-infused material features and build massive datasets of statistically equivalent feature representations of the inherent stochasticity. Classic reconstruction approaches often rely on image pixel-based correlation functions which are typically slow and memory intensive. we developed innovative geometric descriptor and spectral density function methods to statistically represent random material features (e.g., morphology, geometry, and composition) with significant dimension reduction, such that the computational time of reconstruction is reduced from hours to seconds. Such methods are promising for many applications, e.g., manufacturing defect inspection, material repository development, and experimental data augmentation.

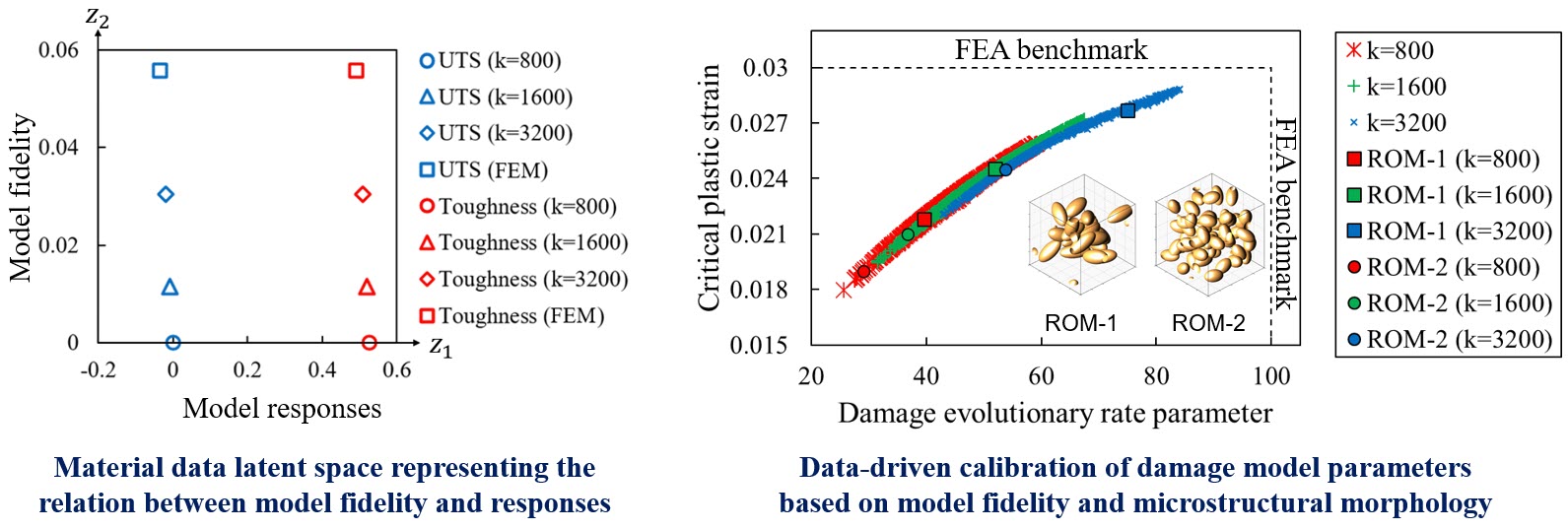
Reduced Order Model: To correlate microstructures with their mechanics performance, we need to numerically assess the effective property of each sample in the material dataset. However, classic direct numerical simulations, e.g., finite element analysis (FEA), are often challenged by numerical issues such as high costs, mesh dependency, and slow convergence for modeling high nonlinearity and path-dependent material behaviors. To address such issues, we developed novel mechanistic reduced-order models (ROMs) that ensembles several contributions to simulate the behavior of spatially varying microstructures under irreversible deformations, including: (𝑖) Data compression that reduces unknown variables by decomposing computational domain into a small number of material clusters, (𝑖𝑖) Deflation algorithm that projects high-dimensional variables into lower dimensional spaces, and (𝑖𝑖𝑖) Explicit-implicit constitutive integration that guarantees positive-definiteness of stiffness matrices with adjustable temporal-spatial discretization for elastoplastic and damage simulations. Such ROMs provide dramatic acceleration for many outer-loop applications, e.g., design optimization, fast dataset generation, uncertainty quantification, and digital twins.

Research Thrust Two: Design Representation

Data-Driven Surrogate: While classic mechanistic models (e.g., homogenization-based multiscale FEA models) provide fundamental understanding of continuum mechanics and facilitate material innovation, they are generally too expensive for the design of multiscale material-structure systems (e.g., composites, alloys, hydrogels, or polymers) across spatial-temporal scales in high dimensional design spaces. In this research, by data mining the massive datasets of stochastic microstructures with their associated anisotropic properties, we developed a physics-informed deep learning surrogate to efficiently emulate the effective responses of heterogeneous microstructures under irreversible plastic deformation with hardening and softening behaviors. It demonstrated a significant accuracy improvement over pure data-driven ‘black-box’ models and a dramatic efficiency boost of about four orders of magnitude of acceleration than FEA.

Material Data Assimilation: In data-centric design, one important question is: Given the limited amount of engineering data, how can we address the data reliance challenges, such as lack of data, low-quality data, and data interpretability? To answer this question, we developed a robust statistical learning model to assimilate data from multiple sources and constructed a multi-fidelity scheme to calibrate the parameters of low-fidelity models as a function of microstructural morphology and data fidelity. The data assimilation scheme not only reduces data reliance on expensive high-fidelity samples by systematically fusing cheap low-fidelity data, provides interpretable latent spaces and quantifies material informatics via statistical sensitivity analysis, but also shows promising potential to augment numerical-experimental datasets to build large material repositories for future material discovery.

Research Thrust Three: Design Optimization

Topology Optimization (TO) aims to maximize structural performance by optimizing material layouts. However, one of the critical challenges that hinders TO from evolving into widespread industrial applications is the high cost of large-scale models and the complexity of multiple conflicting constraints. We addressed this challenge in a two-step manner. Firstly, we answered the question ‘Given an existing design, is it really worth a computationally intensive TO for a new design?’ by predicting the benefits of potential TO. Then, we developed a topological level-set method that, for the very first time, systematically combined topological sensitivity, level-set, augmented Lagrangian, and HPC. It guarantees unambiguous manufacturing-ready design and dramatically shortens computational time (hours to minutes reduction) for 3D large-scale designs with millions of degrees of freedom. It was further extended to multi-physics designs where TO adjoints of various thermal quantities of interest were derived to improve optimization efficiency.

Data-Driven Metamaterial Design: Metamaterials have garnered substantial attention because they offer a new paradigm in achieving structure-property relationships over a large spectrum of applications (e.g., optical, thermal, and mechanical properties). However, most metamaterial investigations have been restricted to periodic architectures with perfect symmetry which are highly sensitive to inevitable manufacturing defects. In this line of research, we developed a data-driven multiscale design approach that integrated neural networks-based TO with data-driven surrogates to design aperiodic bio-inspired spinodal metamaterials with tunable anisotropy for energy absorption applications, e.g., impact-resistant armors.

publications

Predicting the Benefits of Topology Optimization

Deng, Shiguang, and Krishnan Suresh, Proceedings of the ASME 2015 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Volume 2A: 41st Design Automation Conference, August 2015

Topology Optimization under Linear Thermo-Elastic Buckling

Deng, Shiguang, and Krishnan Suresh, Proceedings of the ASME 2016 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Volume 1A: 36th Computers and Information in Engineering Conference, August 2016

talks

teaching